Zu einer logarithmischen Musiktheorie

Zusammenfassung: Die komplexen Töne, die in der ethnischen Musik der Schweiz verwendet werden, entsprechen der harmonischen Abfolge der Resonanzmoden von Wellenleitern. Diese Töne stellen sich als diskrete logarithmische Kurve dar. Die Abbildung auf positive ganze Zahlen ergibt eine andere Art der Nummerierung von Tonleitern, wie sie in der westlichen Musik üblich ist. Mit diesem Ansatz ist es möglich, einen Schweizer Naturjodler oder eine Schweizer Hornmelodie, einen Teil davon oder auch nur ein Motiv als endliche Folge von positiven ganzen Zahlen zu interpretieren. Die Auseinandersetzung mit der Menge der natürlichen Zahlen öffnet neue Möglichkeiten für mathematische Erkenntnisse und musikalische Umsetzung.

Temperierte Stimmung als lineares Modell

Seit der Einführung der gleichstufigen Stimmung durch Simon STEVIN [NL, 1548-1620], die 1605 in Van de spiegheling der singconst veröffentlicht wurde, ist eine 12-tönige gleichstufige Stimmung zur Standardstruktur der europäischen klassischen Musik geworden. Daraus wurde die gesamte Harmonilehre abgeleitet.

Die Stapelung von 12 reinen Quinten (Frequenzverhältnis 3:2) übereinander ergibt die folgende Sequenz

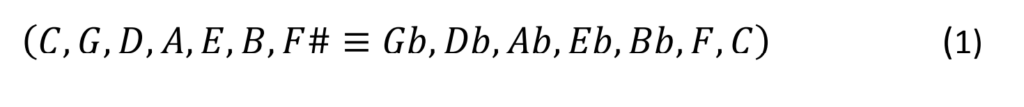
welche allerdings 7 Oktaven (Frequenzverhältnis 2:1) geringfügig übersteigt. Sieben Oktaven ergeben 8400 Cent, aber zwölf reine Quinten ergeben 8423,46 Cent. Die Differenz von ∆= 23,46 Cent wird als pythagoreisches Komma bezeichnet. Oder im Verhältnis

Die bekannte Lösung für diese Abweichung besteht darin, sie gleichmäßig auf jede der 12 Quinten zu verteilen. Mit dieser kleinen Korrektur von 2 Cent pro Quinte gelingt es, die Natur zu überlisten. (vgl. auch Tabelle 1) Und dieses lineare Modell von 12 Halbtönen mit einem Verhältnis von jeweils 2^(1/12) hat sich sehr bewährt; der Nachteil leicht verstimmter Quinten und folglich anderer temperierter Halbtöne wird durch den wesentlichen Vorteil einer störungsfreien Modulation kompensiert.

Projiziert man nun den obigen Quintenzirkel auf eine Oktave, erhält man

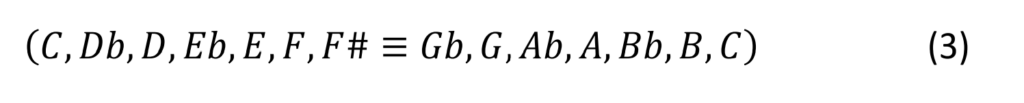
die in der Musiknotation der bekannten chromatischen Tonleiter entspricht

Wenn man diese Klassen von 12 Tonhöhen Zahlen zuordnet, erhält man

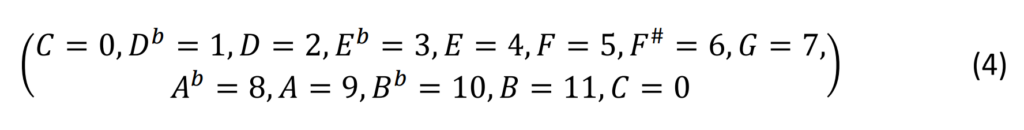
Damit haben wir eine Abbildung der chromatischen Tonleiter auf die ganzen Zahlen mod 12, d.h. ℤ₁₂, erreicht. Dieses ganzzahlige Modell mit Transposition und Inversion ist in [1] gut beschrieben.

Natürliche Resonanzmodi [NRMs]

Zur gleichen Zeit, als STEVIN die temperierte Stimmung propagierte, erfand Jost BÜRGI [CH, 1552 – 1632], ca. 1600 die Logarithmen. Diese wurden später duch John NAPIER [GB, 1550 – 1617] in Mirifici Logarithmorum Canonis Descriptio (1614) und Henry BRIGGS [GB, 1561 – 1630] in (1617) international bekannt gemacht.

Betrachten wir nun das Überblasen eines Schweizer Horns (gebogen, gefaltet oder gerade – Alphorn, Büchel, Tiba), das die folgenden musikalischen Töne k (natürliche Resonanzmoden = NRMs, Obertöne, ‚les harmoniques‘, ‚Naturtoene‘) [2] mit ihrer entsprechenden mathematischen diskreten logarithmischen Kurve aufweist:

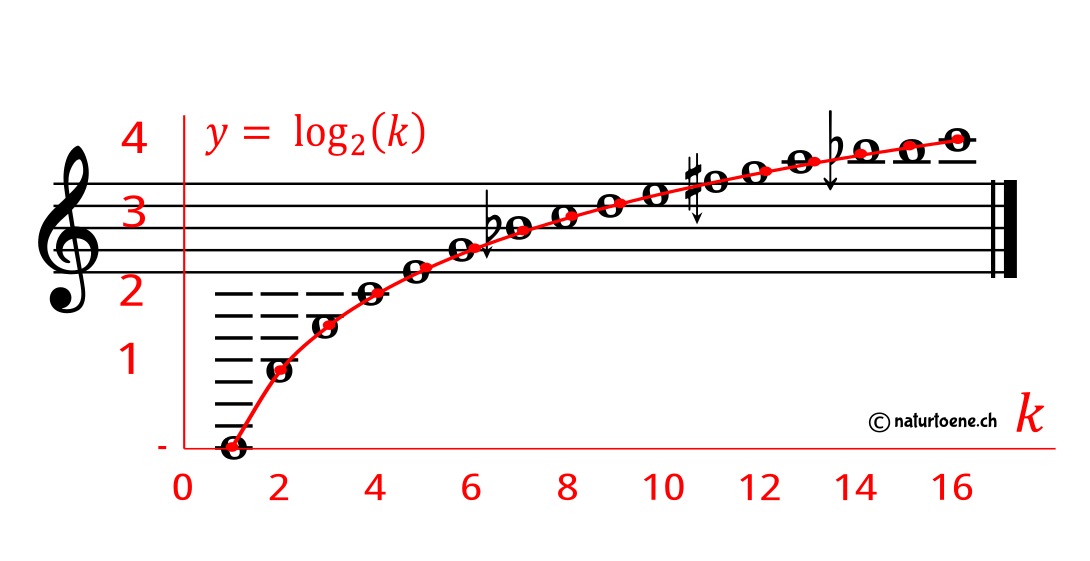
Der Autor hat gezeigt, dass sogar 32 der natürlichen Resonanzmodi – welche den ersten 5 Oktaven entsprechen – spielbar und messbar sind [3]:

Naturton					Dichtestes ET-Intervall	ET Note	Cts
1	2	4	8	16	Prime (Oktave)	C	0
				17	kleine Sekunde	C#, Db	+5
			9	18	große Sekunde	D	+4
				19	kleine Terz	Dis, Es	-2
		5	10	20	große Terz	E	-14
				21	vierte	F	-29
			11	22	Tritonus	Fis, Gb	-49
				23	Tritonus	Fis, Gb	+28
	3	6	12	24	fünfte	G	+2
				25	kleine Sexte	G#, Ab	-27
			13	26	kleine Sexte	G#, Ab	+41
				27	große Sexte	A	6
		7	14	28	kleine Septime	A#, Bb	-31
				29	kleine Septime	A#, Bb	+30
			15	30	große Septime	B	-12
				31	große Septime	B	+45

Aus der Perspektive des logarithmischen Modells unterscheiden sich die Halbtöne bis zur fünften Oktave bis zu einem Viertelton (=50 Cent), was leicht hörbar ist! Weitere Informationen zur Hörfähigkeit des menschlichen Ohrs siehe [4].

Mehr Harmonien in der Höhe

Betrachten wir einige interessante Merkmale der logarithmischen Skala – der „Mutter aller Skalen“. Dabei sticht zunächst der Unterschied zwischen dem NRM- und dem EDS-System bei der Nummerierung ins Auge. Im Gegensatz zum linearen Modell, wo man die Zahl 5 mit den Quinten und die 3 mit den großen Terzen assoziiert, ist hier im System der NRM die Quinte die 3 und die große Terz die 5. Diese Nummerierung hat den grundsätzlichen Vorteil einer konsistenten Berechnung: z.B. ist die Neun = 9 in Wirklichkeit die Stapelung von 2 „Quinten“, d.h. 3^2 = 9, weil die Multiplikation in einem logarithmischen System einer Addition entspricht. Ebenfalls ist folgendes zu beachten:

• Oktaven liegen jeweils zwischen den beiden Töne 2^𝑘 und 2^𝑘+1, (𝑘 ∈ ℕ)
• Die Dichte der Töne (= Anzahl der Töne innerhalb einer Oktave) ist gegeben durch d = 2^𝑘-1, (𝑘 ∈ ℕ)
• Die Gesamtzahl der Töne pro Oktave ist also n = d+2= ^2𝑘+1, (𝑘 ∈ ℕ)
• Der Anstieg der möglichen Intervalle ist durch den Binomialkoeffizienten gegeben:

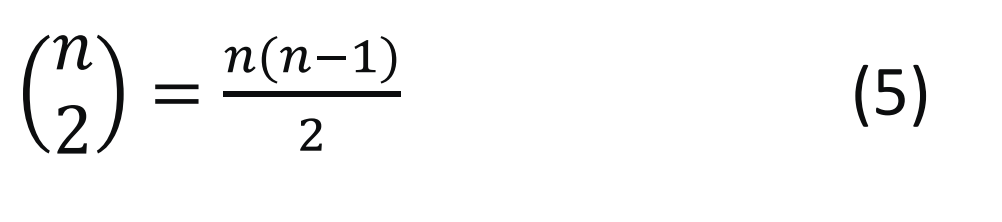
Allgemeiner ausgedrückt: Die Anzahl der möglichen m-Akkorde (wobei m die Anzahl der Töne im Akkord ist) kann für jede Oktave mit dem Binomialkoeffizienten 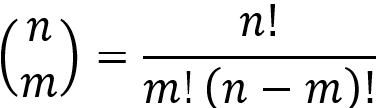berechnet werden:

Mögliche m-Akkorde	Oktave (n)
m	1 (2)	2 (3)	3 (5)	4 (9)	5 (17)
2er-Akkorde (Intervalle)	1	3	10	36	136
3er-Akkorde		1	10	84	680
4er-Akkorde			5	126	2’380
5er-Akkorde			1	126	6’188
6er-Akkorde				84	12′376
7er-Akkorde				36	19′448
8er-Akkorde				9	24′310
9er-Akkorde				1	24′310

Der unverkennbare Klang der Primzahlen

Die Primzahlen ℙ sind nicht nur der ultimative Rahmen für die positiven ganzen Zahlen ℕ, sondern es gibt auch eine Eins-zu-Eins-Entsprechung zwischen der mathematischen Nummerierung und der physikalischen Realität: in dem Sinne, dass im logarithmischen Modell nur die Primzahlen eine neue physikalische Klangfarbe/Qualität hinzufügen. Dies ist auf das unterschiedliche Abstrahlverhalten der Schallwellen zurückzuführen [5]. Die zusammengesetzten Zahlen sind eigentlich nur eine Kombination von 2 Intervallen, wie z.B. 10 = 5 ∙ 2, was eine „Terz“ ist, die zu einer Oktave hinzugefügt wird, mit anderen Worten nichts Neues. Oder 15 = 5 ∙ 3, d.h. eine „große Terz“, die auf eine „Quinte“ addiert wird und eine große Septime ergibt.

Es ist bekannt, dass zusammengesetzte Zahlen in Rechtecken angeordnet werden können, Primzahlen jedoch nicht:

Die Zahlen der Resonanzmodenskala lassen sich als logarithmische Spirale darstellen – jede Umdrehung entspricht einer Oktave. Mit jeder neuen Oktave kommen zusätzliche Noten hinzu. Aber nur Primzahl-Töne geben einen neuen Klang! Sie können nicht mit den bestehenden Tönen konstruiert werden.

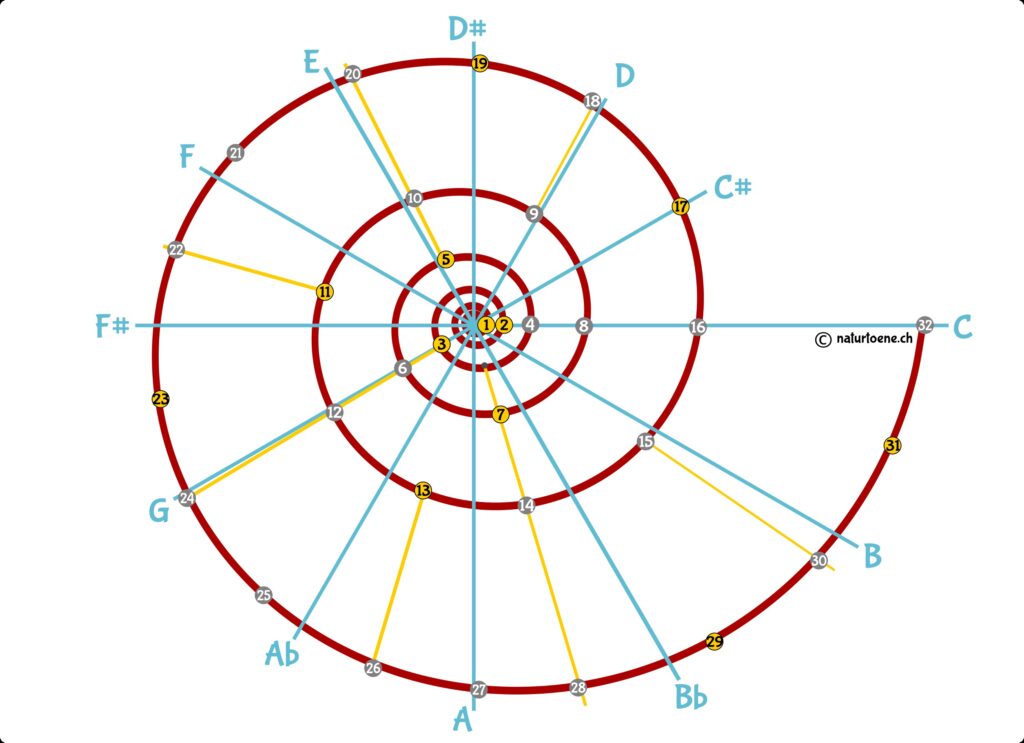
Schauen wir uns die verschiedenen Oktaven der NRMs genauer an: Alle geradzahligen Töne sind wiederholte Töne und daher zusammengesetzt, die ungeradzahligen Töne sind entweder Primzahlen oder zusammengesetzt.

1. Die erste Oktave enthält keine Töne
2. Die zweite Oktave enthält einen zusätzlichen Ton: die 3 = „Quinte“ (!), die eine Primzahl ist.
3. Die dritte Oktave hat den Ton Nr. 3 – einfach eine Oktave höher – wiederholt 6=3∙2. Dieses Phänomen der Oktavverschiebung der „alten“ Töne ist eine generelle Tatsache der NRMs. Aber es gibt auch zwei neue zusätzliche Töne: den dritten =5 (!) und den siebten =7, die zu „neuen“ Tönen führen. Die „Neuheit“ dieser Töne ist physikalisch durch eine neue Klangqualität und mathematisch durch eine Primzahl gekennzeichnet!
4. In der vierten Oktave – neben der Wiederholung der Töne der vorherigen Oktave, d.h. der oktavverschobenen „Terz“, der doppelten oktavverschobenen „Quinte“ und der oktavverschobenen Septime (10 = 5∙2, 12=3∙2^2 , 14=7∙2) – haben wir auch die ungeraden zusätzlichen vier Tonzahlen 9, 11, 13 & 15. Aber nur die beiden Primzahltöne 11 und 13 sind wirklich neu! Denn 9=3^2 und 15 =3∙5, d. h. zwei gestapelte „Quinten“ und eine „Quinte“ + eine „große Terz“, sind mit anderen Worten zusammengesetzt.
5. In der fünften Oktave gibt es acht ungerade Zusatztöne: 17, 19, 21, 23, 25, 27, 29, 31. Von ihnen sind nur die Primzahlen 17, 19, 23, 29 und 31 neu! Denn die Zahlen 21=7∙3, 25=5^2 und 27=9∙ 3 = 3^3 sind alle zusammengesetzt. Und die wiederholten Töne sind auch alle gerade wie üblich 18 = 9∙2, 20=10∙2, 22=11∙2, 24=12∙2, 26=13∙2, 28=14∙2, 30 = 15 ∙ 2

Alles in allem: Nur die Primzahltöne sind das Grundgerüst der natürlichen Resonanztöne.

Zahlentheoretische Analyse von musikalischen NRM-Beispielen

Hier wird nur die Tonhöhe der Melodie berücksichtigt; eine zeitliche mathematische Beschreibung findet sich in [7]. Bevor wir uns einige Beispiele der ethnischen Musik der Schweiz ansehen, werfen wir einen Blick auf die 3. Oktave: Der interessante Ton ist die 7, die bekannte Natur- oder Blues-Septime, die tiefer ist als die Dominantseptime des EDS [= equal
division system; gleichstufige Stimmung]. Wenn wir die 4. Oktave betrachten, haben wir die 11 ≡ das Horn-𝑓𝑎, die 13 ≡ das Horn-𝑙𝑎 und die 14 ≡ 7. Diese Töne sind nicht nur deshalb etwas Besonderes, weil es sich um Primzahlen handelt und sie eine neue Klangqualität haben, sondern auch, weil sie für Menschen, die an 12 Halbtöne gewöhnt sind, seltsam klingen.

Beispiel 1: Dr Sunnehäubeler

In diesem zweitstimmigen Musikstück kommen alle oben genannten Töne 7, 11 und 13 in der 2. Stimme vor:

Betrachtet man den zweiten Teil (B1) des traditionellen Schweizer Naturjodlers „Dr Sunnehäubeler“, so ergeben sich folgende Zahlenfolgen:

Die Hauptmelodie (zweite Zeile) enthält die interessanten Töne 14 ≡ 7, 11 und 13. Wie passen sie mit der zweiten Stimme zusammen? Welche Art von Intervallen erhalten wir? Bestimmt man den größten gemeinsamen Teiler durch Primfaktorzerlegung oder den EUKLIDschen-Algorithmus [8], so kann man sagen, dass, solange es einen größten gemeinsamen Teiler gcd(𝑛₁,𝑛₂) von zwei Tönen 𝑛₁ und 𝑛₂ in einem vertikalen 2D-Vektor [𝑛₁,𝑛₂]‘ gibt, wir nur Standardharmonien erhalten. Aber immer dann, wenn gcd(𝑛₁,𝑛₂) = 1 ist, wie z.B. bei [10, 13]‘, [9, 14]‘ und [11,13]‘, d.h. wenn die Tonzahlen relativ prim sind, entstehen neue und interessante Intervalle (Harmonien).

Beispiel 2: Ranz des Vaches de Fribourgois

Erweitern wir die obige Analyse auf ein 3D-Beispiel, d.h. betrachten wir die ersten 10 Takte des ersten Teils der berühmten Kuhsequenz „Ranz des vaches Fribourgeois“ und deren entsprechenden Nummern.

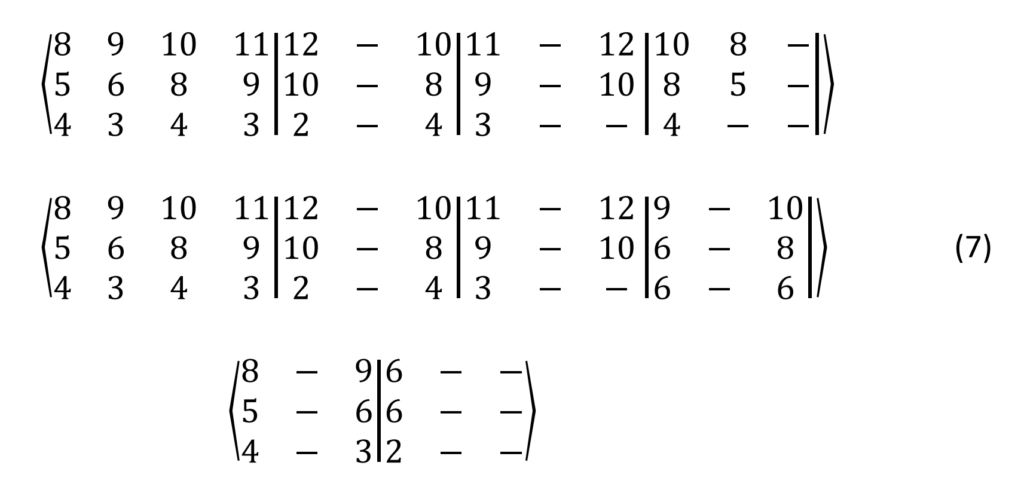
Im Falle einer dreistimmigen Melodie untersuchen wir die drei Tonzahlen 𝑛1_,𝑛₂ und 𝑛₃. Der vertikale 3D-Vektor oder die Anordnung [𝑛₁ 𝑛₂ 𝑛₃]‘ stellt einen Dreiklangsakkord dar. Der gcd von drei oder mehr Tonzahlen ist gleich dem Produkt der gemeinsamen Primfaktoren aller Zahlen, kann aber auch durch wiederholtes Bilden der gcds von Zahlenpaaren berechnet werden:

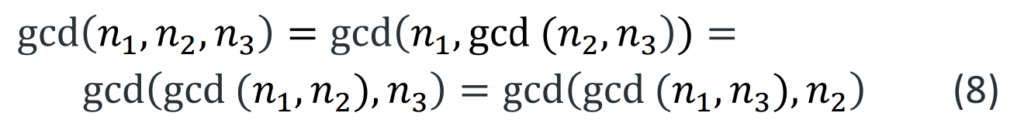
Schauen wir uns einige Beispiele an:

• gcd(8,5,4) = 1 (d.h. kein gemeinsamer Teiler) : Diese 3 ganzen Zahlen sind zueinander relativ prim. Sie sind jedoch nicht paarweise relativ prim, denn gcd(8,5) = 1, gcd(8,4) = 4, gcd(5,4) = 1
• gcd(9,6,3) = 3
• gcd(10,8,4) = 4
• gcd(11,9,3) = 1 (kein gemeinsamer Teiler)
• gcd(7,11,13) = 1 wäre nicht nur wechselseitig relativ, sondern sogar paarweise relativ prim. Dieses Beispiel zeigt, dass gegenseitige und paarweise relative Primzahlen die wenigsten Standardharmonien ergeben; und es scheint ein großes Feld für weitere spezielle harmonische Klänge mit Primzahlvektoren zu geben.

Die obigen Beispiele zeigen ein in NRMs geschriebenes Musikstück als horizontale (Melodien als zeitliche Sequenzen) und vertikale Vektoren (Akkorde). Der zeitliche Aspekt wurde vom Autor in einem früheren Artikel [7] untersucht und wird – falls erforderlich – auf dieser Plattform weiter erläutert.

Zusammenfassung

Die Untersuchung einiger Beispiele ethnischer Musik der Schweiz hat gezeigt, dass sie eine Grundlage für einen globalen Ansatz globaler ethnischer Kulturen darstellen. Die logarithmische Natur der Resonanzmodi zu musikalischen Tonreihen und Akkorden stellt nicht nur einen verbindenden Ansatz zu verschiedenen anderen europäischen Musikkulturen dar, die auf den natürlichen Resonanzmodi basieren (z.B. Polyphonie Bulgariens, Sardiniens, Norwegens, Frankreichs, Rumäniens, Georgiens, Albaniens), sondern wird hier als ein weltweites ethnomathematisches Konzept vermutet: verschiedene große Kulturen (persische, arabische, subsaharische, indische) haben ihre eigenen endlichen Töne gewählt; jeder Ton, jede Skala, jede Harmonie, jeder regionale Stil kann innerhalb der logarithmischen Folge der Resonanzmodi gefunden werden. Durch die Anwendung der ganzzahligen Zahlen, die den physikalischen Resonanzmodi entsprechen, wird die logarithmische Musiktheorie zu Arithmetik, zu einer mathematischen Ingenieurdisziplin.

Referenzen

[1] FIORE, Thomas : Music and Mathematics, Department of Mathematics and Statistics, University of Michigan-Dearborn
[2] JOHNSTON, Ian (2002): Measured tones, Institute of physics, Bristol & Philadelphia
[3] FEHLMANN, Rolphe F. (1994): Computer simulations and applications of numerical techniques for acoustic waves in curved Swiss horn, PhD thesis, NTH Trondheim, Norway
[4] FEHLMANN, Rolphe F. (2012): A mathematical approach to Swiss natural yodels 1, in: GVS Bulletin 2012, publication of the Swiss Society for Ethnomusicology CH-EM
[5] FEHLMANN, Rolphe F. (1998): Elliptic wave radiation from curved waveguides, in: Proceedings of ICA 1998, June 20-26, Seattle
[6] WEBER, Benno (2024): Kunstwerk von naturtoene.ch.
[7] FEHLMANN, Rolphe F. (2014): A mathematical approach to Swiss natural yodels 2, in: GVS Bulletin 2014, publication of the Swiss Society for Ethnomusicology CH-EM