Abstract: The complex tones used in Swiss ethnic music correspond to the harmonic sequence of waveguide resonance modes. These musical tones turn out to be a discrete logarithmic curve. The mapping of them onto positive integers produces a different way of counting scales as is usually used in western music. Using this approach it is possible to interpret a Swiss natural yodel or Swiss horn melody, part of it or even just a motif as a finite sequence of positive integers. Working with the set of natural numbers opens new doors for mathematical insights and treatment .
Equal Temperament as the Linear Model
Ever since the introduction of the equal temperament by Simon STEVIN [NL, 1548-1620], published 1605 in Van de spiegheling der singconst, a 12-tone equally spaced chromatic scale has become the standard musical structure for the European classical music, and all the further theory has been emanated from it.
Stacking 12 pure fifths (frequency ratio 3:2) upon each other produces the following sequence
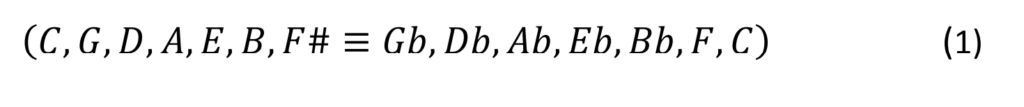
which overshoots 7 octaves (frequency ratio 2:1) by a small amount. Unfortunately there is this small gap: seven octaves produce 8400 cents, but twelve pure fifths amount to 8423.46 cents. The difference of ∆= 23.46 cents is called the Pythagorean comma. Or in ratio

The well-known solution to this deviation is to distribute it evenly in each of the 12 fifths. With this small correction of 2 cents per fifth, it succeeds in outwitting the nature. (cf. also table 1) And this linear model of 12 semitones with a ratio of 2^(1/12) each has been very successful; the drawback of slightly out of tune fifths and consequently other tempered semitones is compensated by the essential advantage of trouble free modulation.
Now, projecting the above cycle of fifths onto one octave we get
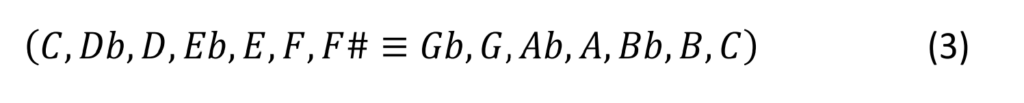
which corresponds in musical notation to well-known chromatic scale

Associating numbers to these 12 pitch classes, we have
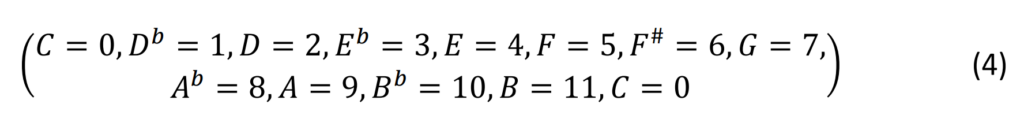
Thus, we have achieved a mapping of the chromatic scale to the integer numbers mod 12 i.e. ℤ12. This integer model with transposition and inversion is well established in [1].
Natural Resonance Modes [NRMs]
During the same period as STEVIN propagated the equal temperament, Jost BÜRGI [CH, 1552 – 1632], invented ca. 1600 the logarithm made internationally known by John NAPIER [GB, 1550 – 1617] in Mirifici Logarithmorum Canonis Descriptio (1614) and Henry BRIGGS [GB, 1561 – 1630] in (1617).
Now, consider the overblowing of a Swiss horn (curved, folded or straight – Alphorn, Büchel, Tiba) exhibiting the following musical tones k (natural resonance modes = NRMs, overtones, ‘les harmoniques’, ‘naturtoene’) [2] with their corresponding mathematical discrete logarithmic curve:
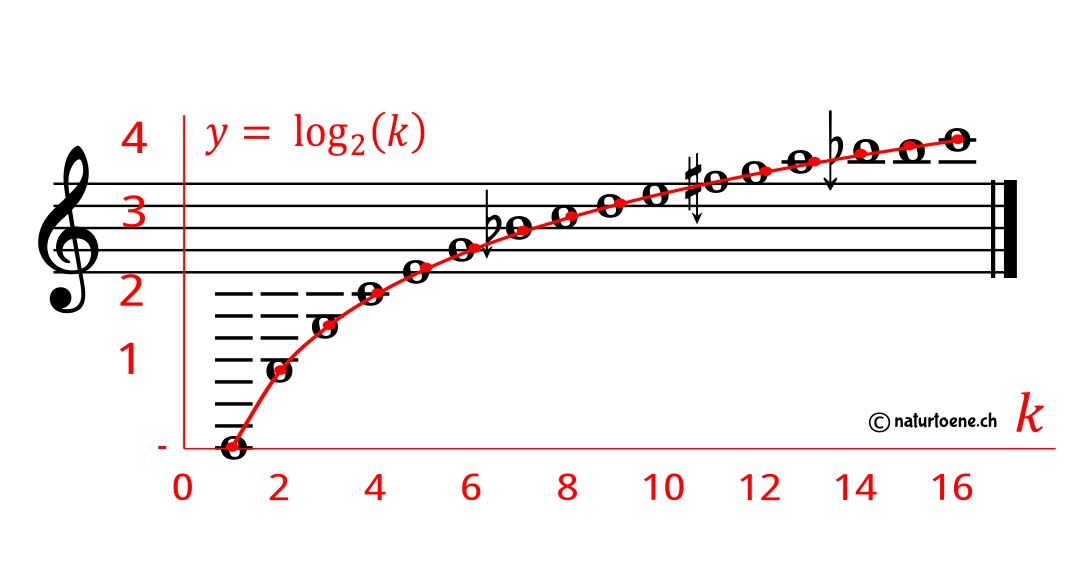
The author has shown that even 32 of the natural resonance modes corresponding to 5 octaves are playable and measurable [3]:

Fig. 3: The first 32 resonance modes of a Swiss horn (curved, folded or straight); prime numbers are
highlighted. In the Swiss ethnic tradition, the musical notes are actually referred to by numbers.
Let’s us look at the difference in cents (cts) between this logarithmic and the linear model:
| Harmonic | Closest ET interval | Note | Cts | ||||
| 1 | 2 | 4 | 8 | 16 | prime (octave) | C | 0 |
| 17 | minor second | C#, Db | +5 | ||||
| 9 | 18 | major second | D | +4 | |||
| 19 | minor third | D#, Eb | -2 | ||||
| 5 | 10 | 20 | major third | E | -14 | ||
| 21 | fourth | F | -29 | ||||
| 11 | 22 | tritone | F#, Gb | -49 | |||
| 23 | tritone | F#, Gb | +28 | ||||
| 3 | 6 | 12 | 24 | fifth | G | +2 | |
| 25 | minor sixth | G#, Ab | -27 | ||||
| 13 | 26 | minor sixth | G#, Ab | +41 | |||
| 27 | major sixth | A | 6 | ||||
| 7 | 14 | 28 | minor seventh | A#, Bb | -31 | ||
| 29 | minor seventh | A#, Bb | +30 | ||||
| 15 | 30 | major seventh | B | -12 | |||
| 31 | major seventh | B | +45 | ||||
division system [=EDS] model in cents.
From the perspective of the logarithmic model, the semitones up to the fifth octave differ up to one quarter tone (=50 cents) which is easy audible! For further information on hearing ability of the human ear, see [4].
Harmonic possibilities increase with pitch
Let us remark some interesting characteristics of the logarithmic scale, the so-called ‘mother of all scales’. To begin with, take notice of the important difference in counting between the NRM and the EDS systems. In contrast to the linear model, where people associate the number 5 to the fifths and the 3 to the major thirds, here in the system of the NRM the fifth is the 3, and the major third is the 5. This numbering has the fundamental advantage of a consistent calculation: e.g. the ninth = 9 is really the stacking of 2 ‘fifths’, i.e. 3^2 = 9, because multiplication in a logarithmic system amounts to an addition. Then besides the different nomenclature we note
- Octaves are delimited by the two tones 2𝑘 and 2𝑘+1, (𝑘 ∈ ℕ)
- The density of tones (= number of tones within the octaves) is given by d = 2𝑘-1, (𝑘 ∈ ℕ)
- Hence, the total number of tones per octave is n = d+2 = 2𝑘+1 , (𝑘 ∈ ℕ)
- The number of possible intervals increases depending on the octave given by the binomial coefficient:
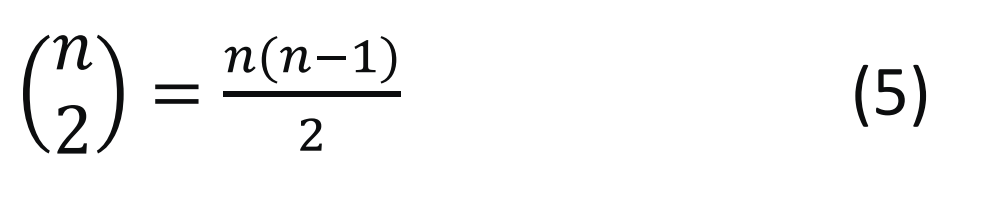
More generally, the number of possible m-chords (where m is the number of tones in the chord) can be calculated for every octave by the binomial coefficient 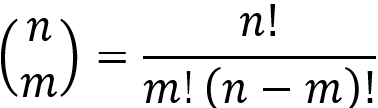 :
:
| Possible m-Chords | Octave (n) | ||||
| m | 1 (2) | 2 (3) | 3 (5) | 4 (9) | 5 (17) |
| 2-chords (interval) | 1 | 3 | 10 | 36 | 136 |
| 3-chords | 1 | 10 | 84 | 680 | |
| 4-chords | 5 | 126 | 2’380 | ||
| 5-chords | 1 | 126 | 6’188 | ||
| 6-chords | 84 | 12′376 | |||
| 7-chords | 36 | 19′448 | |||
| 8-chords | 9 | 24′310 | |||
| 9-chords | 1 | 24′310 | |||
The unique sound of prime numbers
The set of prime numbers ℙ are not only the ultimate framework of the positive integers ℕ, but there is also a one-to-one correspondence between the mathematical numbering and the physical reality: in the sense that in the logarithmic model only prime numbers add a new physical tone flavor/quality. This is due to different radiating sound wave behavior [5]. The composite numbers are really just a combination of 2 intervals like e.g. 10 = 5 ∙ 2, which is a ‘third’ added upon anoctave, in other words nothing new. Or 15 = 5 ∙ 3, that is a ‘major third’ added up on a ‘fifth’ yielding a major seventh.
It is well known that composite numbers can be arranged into rectangles but prime numbers not:

The numbers of the resonance modes scale can be represented as a logarithmic spiral – each turn representing an octave. While ratcheting up, new notes are added. But only prime number notes add a new flavour! They cannot be constructed with the tones already present in the lower pitches.
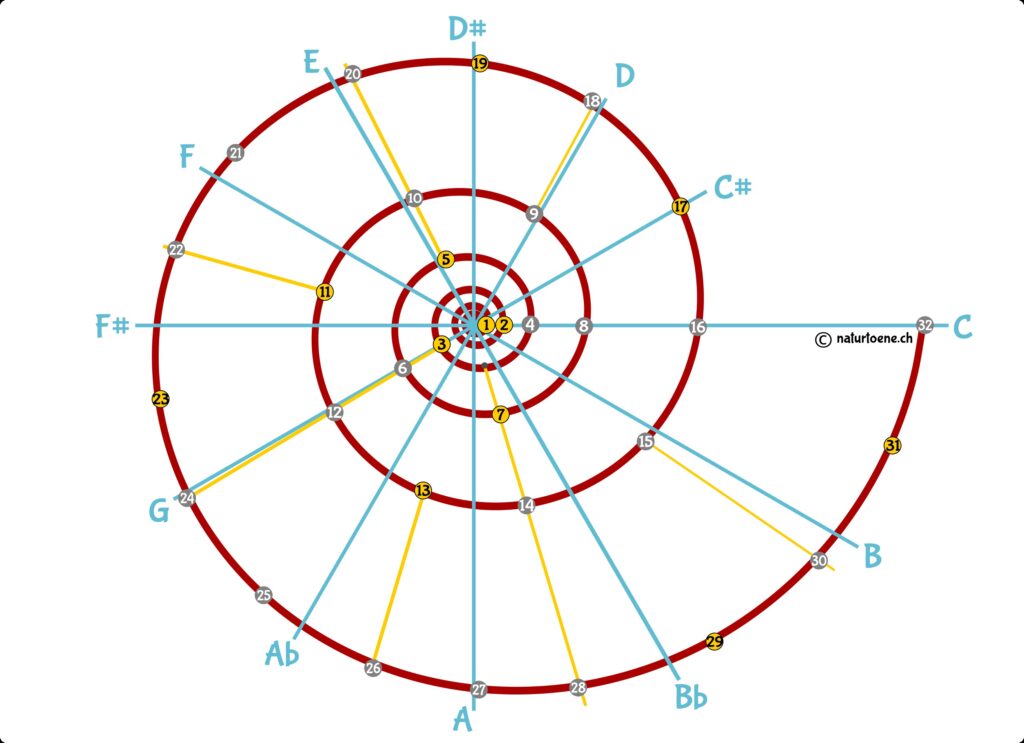
Let’s take a closer look at the different octaves of the NRMs: All even number tones are repeated tones and therefore composite, the odd number tones are either prime or composite.
- The first octave does contain no tones.
- The second octave contains one additional tone: the 3 =’fifth’ (!) which is a prime number.
- The third octave has tone no. 3 just repeated one octave higher 6=3∙2. This phenomenon of octave displacement of the ‘old’ tones is a general fact of the NRMs. But there are also two new additional tones: the third =5 (!) and the seventh =7, which result in ‘new’ tones. The ‘newness’ of these tones are characterized physically by a new quality of sound and mathematically by a prime number!
- In the fourth octave – besides repeating the tones of the former octave, i.e. the octave shifted ‘third’, the double octave shifted ‘fifth’ and the octave shifted seventh (10 = 5∙2, 12=3∙2^2 , 14=7∙2), we also have the odd additional four tone numbers 9, 11, 13 & 15. But only the two prime number tones 11 and 13 are actually new! Because 9=3^2 and 15 =3∙5, i.e. two stacked ‘fifths’ and a ‘fifth’ + a ‘major third’, are in other words composite.
- In the fifth octave, there is eight odd additional tones: 17, 19, 21, 23, 25, 27, 29, 31 From them only the prime numbers 17, 19, 23, 29 and 31 are new! Because the 21=7∙3, 25=5^2 and 27=9∙ 3 = 3^3 are all composite. And the repeated tones are also all even as usual 18 = 9∙2, 20=10∙2, 22=11∙2, 24=12∙2, 26=13∙2, 28=14∙2, 30 = 15 ∙ 2
In all: Only the prime number tones are the fundamental framework of the natural resonance mode tones.
Number Theoretic Analysis of Musical NRM examples
Here only the pitch of the melody is taken into consideration; for a temporal mathematical description, refer to [7]. Before we look at some examples of the Swiss ethnic music tunes, let’s take a closer look at the 3rd octave: the interesting tone is the 7, the well-known natural seventh or Blues seventh which is lower than the dominant seventh of the EDS [= equal
division system]. Considering the 4th octave, we have the 11th ≡ the horn-𝑓𝑎, the 13th ≡ the horn-𝑙𝑎 and the 14th ≡ 7 th. These tones are special not only because they are prime numbers and include a new sound quality, but also because they sound strange to people with a 12-semitone hearing habit.
Example 1: Dr Sunnehäubeler
In this 2-part musical piece all of the above mentioned tones 7, 11 and 13 occur in the B part:

Considering the second part (B1) of the traditional Swiss natural yodel ‘Dr Sunnehäubeler’ we end up with the following sequence of numbers:

The main melody (second line) contain the interesting tones 14 ≡ 7, 11 and 13. How do they fit together with the second voice? What kind of intervals do we get? Determining the greatest common divisor by prime factorization or the EUCLIDean algorithm [8], we can say that as long as there is a greatest common divisor gcd(𝑛1, 𝑛2) of two tones 𝑛1 and 𝑛2 in a vertical 2D vector [𝑛1, 𝑛2]’, we just get standard harmonies. But whenever we have a gcd(𝑛1, 𝑛2) = 1, like e.g. with [10, 13]’, [9, 14]’ and [11,13]’, i.e. when the tone numbers are relatively prime, new and interesting intervals (harmonies) arise.
Example 2: Ranz des Vaches Fribourgeois
If we extend the above analysis to a 3D example, i.e. looking at the first 10 measures of the first part of the famous cow sequence ‘Ranz des vaches Fribourgeois’ and its corresponding numbers.

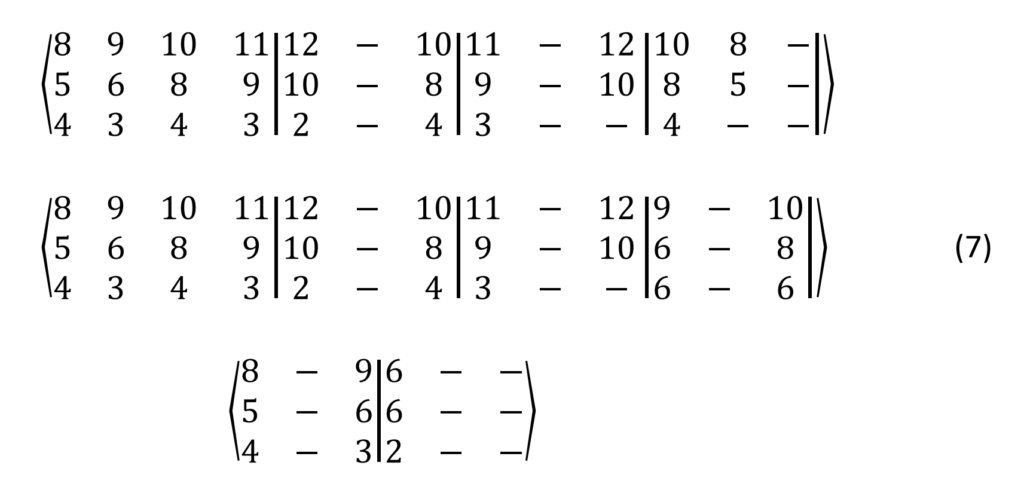
In the case of a 3-part tune, we investigate the three tone numbers 𝑛1, 𝑛2 and 𝑛3. The vertical 3D vector or array [𝑛1 𝑛2 𝑛3]’ represents a triad chord. The gcd of three or more tone numbers equals the product of the prime factors common to all the numbers, but it can also be calculated by repeatedly taking the gcds of pairs of numbers.
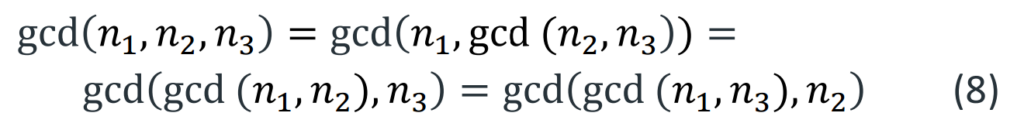
Let’s look a some examples:
- gcd(8,5,4) = 1 (i.e. no common divisor) : These 3 integers are mutually relatively prime. However, they are not pairwise relatively prime, because gcd(8,5) = 1, gcd(8,4) = 4, gcd(5,4) = 1
- gcd(9,6,3) = 3
- gcd(10,8,4) = 4
- gcd(11,9,3) = 1 (no common divisor)
- gcd(7,11,13) = 1 would not only be mutually relatively but even pairwise relatively prime. This example shows that mutually and pairwise relatively prime numbers yield the least standard harmonies; and there seems to exist a large field for further special harmonic sounds with prime number vectors.
Note that the examples above show a musical piece written in NRMs as horizontal (melodies as temporal sequences) and vertical vectors (chords). The temporal aspect has been investigated by the author in an earlier article [7] and – if necessary – will be further explained on this platform.
Summary
Investigation of some examples of Swiss ethnic music tradition has shown to be a basis for a global approach of ethnic cultures. The logarithmic nature of the resonance modes to musical scales and chords exhibits not only a unifying approach to different other European musical cultures based on the natural resonance modes (e.g. polyphonies of Bulgaria, Sardegna of Italy, Norway, Corse of France, Romania, Georgia, Albania), but is conjectured here to be a worldwide ethno mathematical concept: different great cultures (Persian, Arab, Subsaharan Africa, India, China) have chosen their own specific finite set of tones; any note, any scale, any harmony, any regional style can be found within the logarithmic sequence of the resonance modes. Through application of the integer numbers corresponding to the physical resonance modes, the logarithmic music theory emerges into a calculus, a mathematical engineering discipline.
References
[1] FIORE, Thomas : Music and Mathematics, Department of Mathematics and Statistics, University of Michigan-Dearborn
[2] JOHNSTON, Ian (2002): Measured tones, Institute of physics, Bristol & Philadelphia
[3] FEHLMANN, Rolphe F. (1994): Computer simulations and applications of numerical techniques for acoustic waves in curved Swiss horn, PhD thesis, NTH Trondheim, Norway
[4] FEHLMANN, Rolphe F. (2012): A mathematical approach to Swiss natural yodels 1, in: GVS Bulletin 2012, publication of the Swiss Society for Ethnomusicology CH-EM
[5] FEHLMANN, Rolphe F. (1998): Elliptic wave radiation from curved waveguides, in: Proceedings of ICA 1998, June 20-26, Seattle
[6] WEBER, Benno (2024): Artwork by naturtoene.ch.
[7] FEHLMANN, Rolphe F. (2014): A mathematical approach to Swiss natural yodels 2, in: GVS Bulletin 2014, publication of the Swiss Society for Ethnomusicology CH-EM
Leave a Reply