Vers une théorie logarithmique de la musique

Résumé : Les sons complexes utilisés dans la musique ethnique suisse correspondent à la séquence harmonique des modes de résonance des guides d’ondes. Ces tonalités musicales se révèlent être une courbe logarithmique discrète. Leur mise en correspondance avec des nombres entiers positifs produit une manière différente de compter les gammes, telle qu’elle est habituellement utilisée dans la musique occidentale. Cette approche permet d’interpréter un yodel naturel suisse ou une mélodie de cor suisse, une partie de celle-ci ou même simplement un motif comme une séquence finie d’entiers positifs. Travailler avec l’ensemble des nombres naturels ouvre de nouvelles portes à la compréhension et au traitement mathématiques.

Le tempérament égal comme modèle linéaire

Depuis l’introduction du tempérament égal par Simon STEVIN [NL, 1548-1620], publié en 1605 dans Van de spiegheling der singconst, une gamme chromatique à 12 tons également espacés est devenue la structure musicale standard de la musique classique européenne, et toute la théorie ultérieure en a découlé.

En empilant 12 quintes pures (rapport de fréquence 3:2) les unes sur les autres, on obtient la séquence suivante

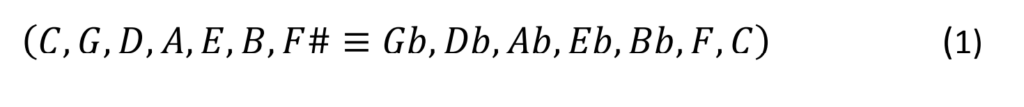
qui dépasse légèrement 7 octaves (rapport de fréquence 2:1). Malheureusement, il y a un petit écart : sept octaves donnent 8400 centimes, mais douze quintes pures donnent 8423,46 centimes. La différence de ∆= 23,46 cents est appelée virgule de Pythagore. Ou en ratio

La solution bien connue à cette déviation est de la répartir uniformément dans chacune des 12 quintes. Avec cette petite correction de 2 centimes par quinte, il réussit à déjouer la nature. (cf. également tableau 1) Et ce modèle linéaire de 12 demi-tons avec un rapport de 2^(1/12) chacun a connu un grand succès; l’inconvénient des quintes légèrement désaccordées et par conséquent d’autres demi-tons tempérés est compensé par l’avantage essentiel d’une modulation sans problème.

En projetant le cycle de quintes ci-dessus sur une octave, on obtient

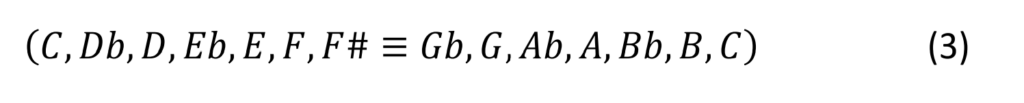
qui correspond, en notation musicale, à la gamme chromatique bien connue

En associant des numéros à ces 12 notes, nous obtenons

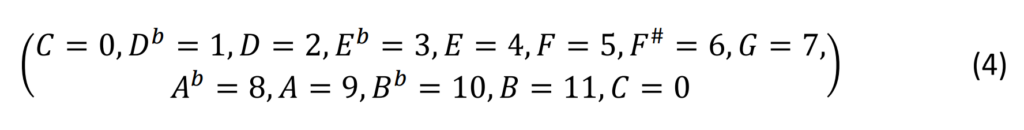
Ainsi, nous avons obtenu une correspondance entre la gamme chromatique et les nombres entiers mod 12, c’est-à-dire ℤ₁₂. Ce modèle de nombres entiers avec transposition et inversion est bien établi dans [1].

Modes de résonance naturelle [NRMs]

Pendant que STEVIN propageait le tempérament égal, Jost BÜRGI [CH, 1552 – 1632], inventait vers 1600 le logarithme rendu connu internationalement par John NAPIER [GB, 1550 – 1617] dans Mirifici Logarithmorum Canonis Descriptio (1614) et Henry BRIGGS [GB, 1561 – 1630] dans (1617).

Considérons maintenant le sursoufflage d’un cor suisse (courbé, plié ou droit – cor des Alpes, Büchel, Tiba) présentant les tonalités musicales k suivantes ( modes de résonance naturels = NRM, harmoniques, « Naturtoene ») [2] avec leur courbe mathématique logarithmique discrète correspondante :

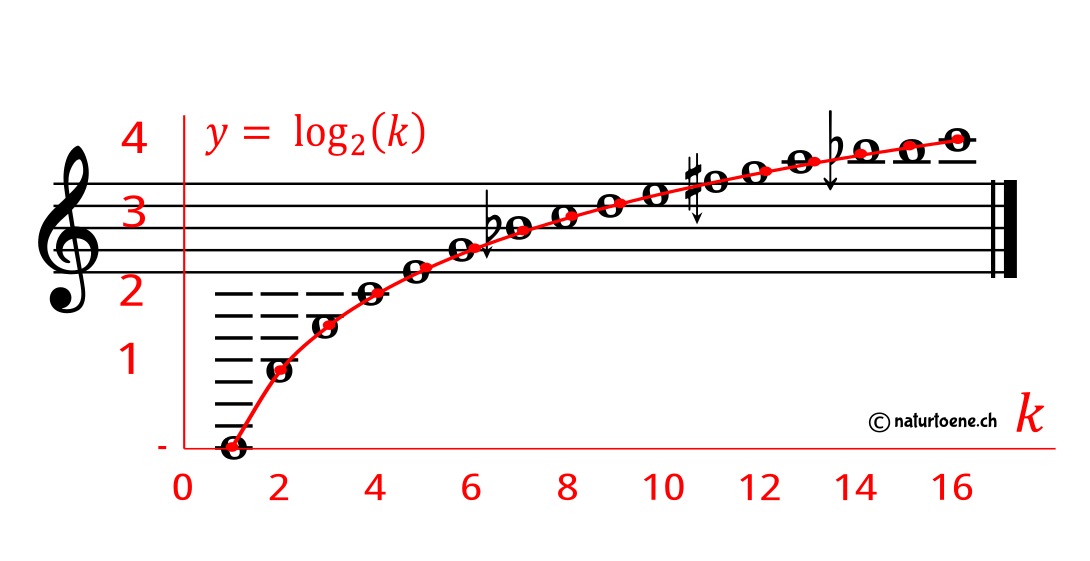
L’auteur a montré que même 32 des modes de résonance naturels correspondant à 5 octaves sont jouables et mesurables [3] :

Harmonique					Intervalle ET le plus proche	Note	Cts
1	2	4	8	16	prime (octave)	Do	0
				17	seconde mineure	Do #	+5
			9	18	grande seconde	Re	+4
				19	tierce mineure	Ré #	-2
		5	10	20	tierce majeure	Mi	-14
				21	Quarte	Fa	-29
			11	22	triton	Fa #	-49
				23	triton	Fa #	+28
	3	6	12	24	Quinte	So	+2
				25	Sexte mineure	So #	-27
			13	26	Sexte mineure	So #	+41
				27	Sexte majeure	La	6
		7	14	28	Septe mineure	La #, Ti b	-31
				29	Septe mineure	La #, Ti b	+30
			15	30	Septe majeure	Ti	-12
				31	Septe majeure	Ti	+45

Du point de vue du modèle logarithmique, les demi-tons jusqu’à la cinquième octave diffèrent jusqu’à un quart de ton (= 50 cents), ce qui est facilement audible ! Pour plus d’informations sur la capacité auditive de l’oreille humaine, voir [4].

Les possibilités harmoniques augmentent en altitude

Remarquons quelques caractéristiques intéressantes de l’échelle logarithmique, la « mère de toutes les échelles ». Tout d’abord, il convient de noter la différence importante de comptage entre les systèmes NRM et EDS. Contrairement au modèle linéaire, où les gens associent le chiffre 5 aux quintes et le 3 aux tierces majeures, dans le système du NRM, la quinte est le 3 et la tierce majeure est le 5. Cette numérotation présente l’avantage fondamental d’un calcul cohérent : par exemple, la neuvième = 9 est en réalité l’empilement de deux « quintes », c’est-à-dire 3^2 = 9, parce que la multiplication dans un système logarithmique équivaut à une addition. Outre la différence de nomenclature, nous notons

• Les octaves sont délimitées par les deux tons 2^𝑘 et 2^𝑘+1, (𝑘 ∈ ℕ).
• La densité des tons (= nombre de tons dans les octaves) est donnée par d = 2^𝑘-1, (𝑘 ∈ ℕ)
• Par conséquent, le nombre total de tons par octave est n = d+2= 2^𝑘+1, (𝑘 ∈ ℕ).
• Le nombre d’intervalles possibles augmente en fonction de l’octave donnée par le coefficient binomial :

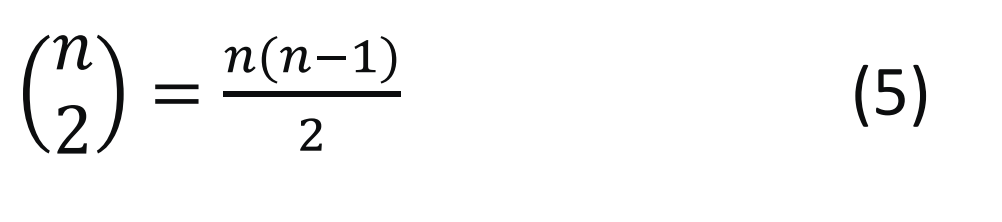
Plus généralement, le nombre d’accords m possibles (où m est le nombre de tons dans l’accord) peut être calculé pour chaque octave par le coefficient binomial :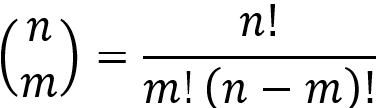

Accords m possibles	Octave (n)
m	1 (2)	2 (3)	3 (5)	4 (9)	5 (17)
2 notes (intervalle)	1	3	10	36	136
3 notes		1	10	84	680
4 notes			5	126	2’380
5 notes			1	126	6’188
6 notes				84	12′376
7 notes				36	19′448
8 notes				9	24′310
9 notes				1	24′310

Le son unique des nombres primaires

L’ensemble des nombres premiers ℙ n’est pas seulement le cadre ultime des entiers positifs ℕ, mais il existe également une correspondance biunivoque entre la numérotation mathématique et la réalité physique: dans le modèle logarithmique, seuls les nombres premiers ajoutent un nouveau timbre / une nouvelle qualité à la tonalité physique. Cela est dû à la différence de comportement des ondes sonores rayonnantes [5]. Les nombres composés ne sont en fait qu’une combinaison de deux intervalles, comme par exemple 10 = 5 ∙ 2, qui est une « tierce » ajoutée à l’octave, en d’autres termes rien de nouveau. Ou 15 = 5 ∙ 3, c’est-à-dire une « tierce majeure » additionnée à une « quinte », ce qui donne une septième majeure.

Il est bien connu que les nombres composites peuvent être disposés en rectangles, mais pas les nombres premiers :

Les chiffres de l’échelle des modes de résonance peuvent être représentés comme une spirale logarithmique – chaque tour représentant une octave. De nouvelles notes sont ajoutées en montant de tonalité. Mais seules les notes de nombres primaires ajoutent un nouveau timbre! Ils ne peuvent pas être construits avec les tons déjà présents dans les octaves inférieures.

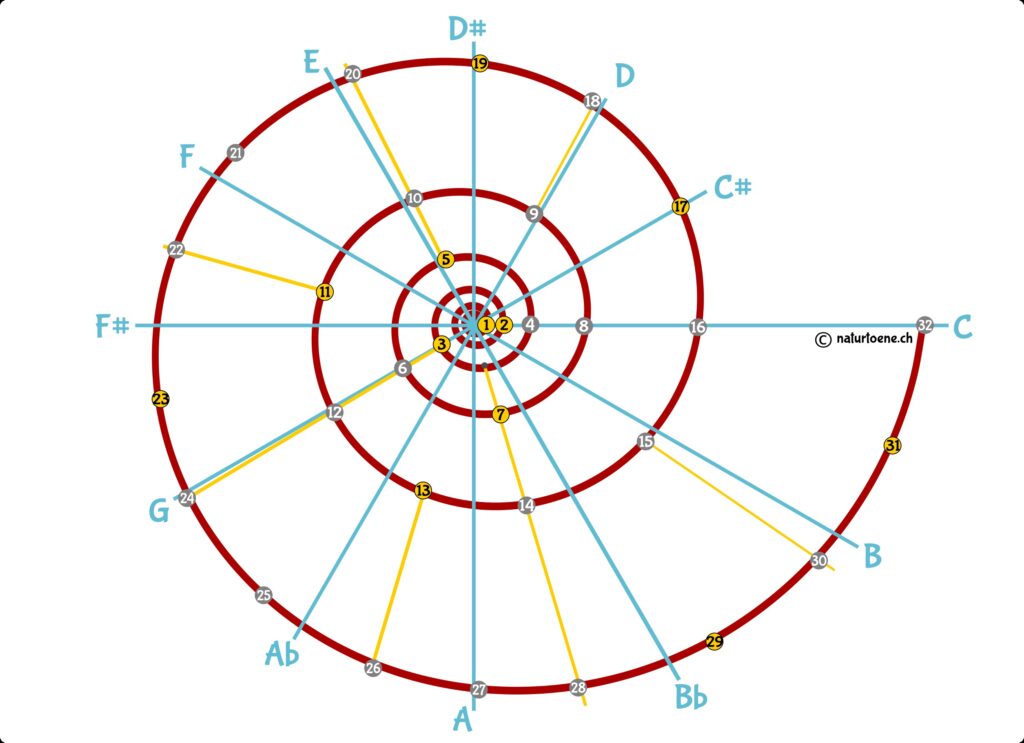
Examinons de plus près les différentes octaves des NRM: Toutes les tonalités paires sont des tonalités répétées et donc composites, les tonalités impaires sont soit premières, soit composites.

1. La première octave ne contient aucun son
2. La deuxième octave contient un ton supplémentaire : le 3 = « quinte » ( !) qui est un nombre premier.
3. La troisième octave a la tonalité n° 3 répétée une octave plus haut 6=3∙2. 3 répété une octave plus haut 6=3∙2. Ce phénomène de déplacement d’octave des « anciennes » tonalités est un fait général des MRN. Mais il y a aussi deux nouveaux tons supplémentaires : la terce =5 ( !) et le sepime =7, qui donnent lieu à de « nouveaux » tons. La « nouveauté » de ces sons est caractérisée physiquement par une nouvelle qualité de son et mathématiquement par un nombre premier !
4. Dans la quatrième octave – outre la répétition des tons de l’octave précédente, c’est-à-dire l’octave décalée « troisième », la double octave décalée « cinquième » et l’octave décalée « septième » (10 = 5∙2, 12=3∙2^2, 14=7∙2), nous avons également les quatre tons supplémentaires impairs 9, 11, 13 & 15. Mais seuls les deux nombres premiers 11 et 13 sont réellement nouveaux ! Car 9=3^2 et 15 =3∙5, c’est-à-dire deux « quintes » empilées et une « quinte » + une « tierce majeure », sont autrement dit composites.
5. Dans la cinquième octave, il y a huit tons impairs supplémentaires : 17, 19, 21, 23, 25, 27, 29, 31 Parmi eux, seuls les nombres premiers 17, 19, 23, 29 et 31 sont nouveaux ! Car les 21=7∙3, 25=5^2 et 27=9∙3=3^3 sont tous composites. Et les tons répétés sont également tous pairs comme d’habitude 18 = 9∙2, 20=10∙2, 22=11∙2, 24=12∙2, 26=13∙2, 28=14∙2, 30=15∙2.

En somme : Seules les tonalités des nombres premiers constituent le cadre fondamental des tonalités du mode de résonance naturel.

Analyse théorique des nombres d’exemples musicaux NRM

Ici, seule la hauteur de la mélodie est prise en considération ; pour une description mathématique temporelle, voir [7]. Avant d’examiner quelques exemples d’airs de musique ethnique suisse, regardons de plus près la 3e octave : le ton intéressant est le 7, la fameuse septième naturelle ou septième de blues, qui est plus basse que la septième dominante de l’EDS.
En considérant la 4e octave, nous avons le 11e ≡ le cor-𝑓𝑎, le 13e ≡ le cor-𝑙𝑎 et le 14e ≡ 7e. Ces sons sont particuliers non seulement parce qu’il s’agit de nombres premiers et qu’ils comportent une nouvelle qualité sonore, mais aussi parce qu’ils sonnent étrangement pour les personnes qui ont l’habitude d’entendre des sons de 12 demi-tons.

Exemple 1 : Dr Sunnehäubeler

Dans cette pièce musicale à deux voix, tous les tons 7, 11 et 13 mentionnés ci-dessus se trouvent dans la partie B :

Si l’on considère la deuxième partie (B1) du jodel naturel traditionnel suisse ‘Dr Sunnehäubeler’, on obtient la séquence de chiffres suivante :

La mélodie principale (deuxième ligne) contient les tons intéressants 14 ≡ 7, 11 et 13. Comment s’articulent-ils avec la deuxième voix ? Quel type d’intervalles obtenons-nous ? En déterminant le plus grand diviseur commun par factorisation des nombres premiers ou par l’algorithme EUCLIDean [8], nous pouvons dire que tant qu’il existe un plus grand diviseur commun gcd(𝑛₁,𝑛₂) de deux tons 𝑛₁ et 𝑛₂ dans un vecteur 2D vertical [𝑛₁,𝑛₂]’, nous obtenons simplement des harmonies standard. Mais lorsque nous avons un gcd(𝑛₁,𝑛₂) = 1, comme par exemple avec [10, 13]’, [9, 14]’ et [11,13]’, c’est-à-dire lorsque les nombres de tons sont relativement premiers, de nouveaux intervalles (harmonies) intéressants apparaissent.

Exemple 2 : Ranz des Vaches de Fribourgois

Si nous étendons l’analyse ci-dessus à un exemple en 3D, c’est-à-dire en regardant les 10 premières mesures de la première partie de la célèbre séquence de la vache « Ranz des vaches fribourgeoises » et les numéros correspondants.

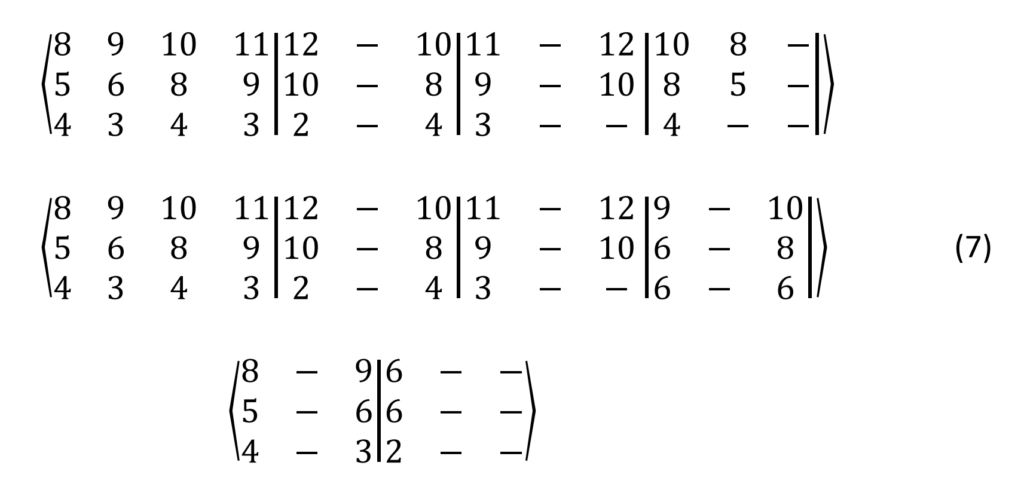
Dans le cas d’une mélodie à trois voix, nous étudions les trois nombres de tons 𝑛₁,𝑛₂ et 𝑛₃. Le vecteur ou tableau vertical 3D [_{𝑛1 𝑛2 𝑛3}]’ représente un accord de triade. Le gcd de trois nombres entiers ou plus est égal au produit des facteurs premiers communs à tous les nombres, mais il peut également être calculé en prenant plusieurs fois le pgcd de paires de nombres.

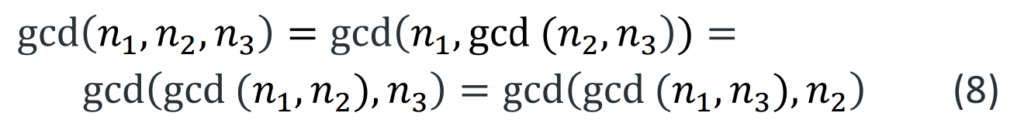
Prenons quelques exemples :

• gcd(8,5,4) = 1 (c.-à-d. pas de diviseur commun) : Ces 3 entiers sont mutuellement relativement premiers. Cependant, ils ne sont pas relativement premiers par paire, car gcd(8,5) = 1, gcd(8,4) = 4, gcd(5,4) = 1.
• gcd(9,6,3) = 3
• gcd(10,8,4) = 4
• gcd(11,9,3) = 1 (pas de diviseur commun)
• gcd(7,11,13) = 1 serait non seulement mutuellement relativement premier, mais aussi relativement premier par paire. Cet exemple montre que les nombres premiers mutuellement et par paire produisent les harmonies les moins standard ; et il semble qu’il existe un vaste champ pour d’autres sons harmoniques spéciaux avec des vecteurs de nombres premiers.

Notez que les exemples ci-dessus montrent une pièce musicale écrite dans des NRM sous forme de vecteurs vecteurs horizontaux (mélodies en tant que séquences temporelles) et vérticaux (accords). L’aspect temporel a été étudié par l’auteur dans un article précédent [7] et – si nécessaire – sera expliqué plus en détail sur cette plateforme.

Résumé

L’étude de quelques exemples de la tradition musicale folklorique suisse s’est révélée être une base pour une approche globale des cultures ethniques mondiales. La nature logarithmique des modes de résonance des gammes musicales et des accords montre non seulement une approche unificatrice des différentes cultures musicales européennes basées sur les modes de résonance naturels (par ex. polyphonies de Bulgarie, Sardegna d’Italie, Norvège, Corse de France, Roumanie, Géorgie, Albanie), mais on suppose ici qu’il s’agit d’un concept ethno-mathématique mondial : différentes grandes cultures (persane, arabe, Afrique subsaharienne, Inde) ont choisi leur propre ensemble fini de tonalités ; toute note, toute gamme, toute harmonie, tout style régional peut être trouvé dans la séquence logarithmique des modes de résonance. En appliquant les nombres entiers correspondant aux modes de résonance physique, la théorie musicale logarithmique devient un calcul, une discipline d’ingénierie mathématique.

Références

[1] FIORE, Thomas : Music and Mathematics, Department of Mathematics and Statistics, University of Michigan-Dearborn
[2] JOHNSTON, Ian (2002): Measured tones, Institute of physics, Bristol & Philadelphia
[3] FEHLMANN, Rolphe F. (1994): Computer simulations and applications of numerical techniques for acoustic waves in curved Swiss horn, PhD thesis, NTH Trondheim, Norway
[4] FEHLMANN, Rolphe F. (2012): A mathematical approach to Swiss natural yodels 1, in: GVS Bulletin 2012, publication of the Swiss Society for Ethnomusicology CH-EM
[5] FEHLMANN, Rolphe F. (1998): Elliptic wave radiation from curved waveguides, in: Proceedings of ICA 1998, June 20-26, Seattle
[6] WEBER, Benno (2024) : Œuvre d’art de naturtoene.ch.
[7] FEHLMANN, Rolphe F. (2014): A mathematical approach to Swiss natural yodels 2, in: GVS Bulletin 2014, publication of the Swiss Society for Ethnomusicology CH-EM